本日読了 興味津々
アイザック・ニュートン は微分積分学の発展に最も貢献した1人であり、万有引力の法則や運動の法則でも微分積分学を応用している。 古代 古代にもいくつかの 積分法 のアイデアは存在したが、厳密あるいは体系的な方法でそれらのアイデアを発展させようという動きは見られない。 積分法の基本的機能である体積や面積の計算は、 エジプト の モスクワパピルス （紀元前10年頃）まで遡り、そニュートンの微積分法ii ニュートンの微積分法ii – p1/14
ニュートン 数学 微分積分
ニュートン 数学 微分積分-ニュートンの業績 1687年 自然哲学の数学的諸原理（プリンキピア） Philosophiae Naturalis Principia Mathematica 微分積分を用いず幾何学的に記述している。 ラテン語で書かれている。 ニュートン力学を完成させた著書。その他様々な命題を含む。 微分積分の論文は？ 微分積分学は、天体の運動を説明するために生まれた 微分積分学を打ち立てたのは、1718世紀の物理学者、アイザック・ニュートンです。 （もう一人、ライプニッツも発見者の一人です。 ） 「落下するリンゴを見て、ひらめいた」という本当かどうか
微分積分学の歴史 理系のための備忘録
ニュートンによる微積分の研究とライプニッツによる研究との間に違いはありますか？ はいの場合は、ポイントごとに言及してください。 # ¿Qué es esta planta en maceta con hojas de color verde oscuro y racimos de flores rojas? 微積分を考えだしたニュートンこそ、まさしく曲線のエキスパート中のエキスパートだったのだから。 1684年8月、ハレーはケンブリッジのニュートンを訪ねた。 決心 結局、ふたりの間にどのようなやりとりがあったのかは謎が多い。AmazonでのNewton別冊『微分と積分 新装版』 (ニュートン別冊)。アマゾンならポイント還元本が多数。作品ほか、お急ぎ便対象商品は当日お届けも可能。またNewton別冊『微分と積分 新装版』 (ニュートン別冊)もアマゾン配送商品なら通常配送無料。
Topics 微積分の創始者をめぐる争い Column 11 あらゆる分野で才能を発揮したライプニッツ Column 12 『プリンキピア』のなぞ―ニュートンは微積分を使ったのか？ Topics 17世紀以降の微積分の発展 3 もっと知りたい！ 微積分の応用 PART 1 基礎編 微分・積分の使い道は「物体の運動を計算すること」です。 と言うのも微分・積分を作ったのは有名な物理学者、ニュートンなのです。 物体の運動を方程式で表すことに成功しました。 です。 （F：力、m：質量、a：加速度） の様に微分を使って書かれ微分や積分の成り立ちが理解できます。これまで数式を暗記したり、なんとなく微分や積分を理解してきた人にとって、おすすめの1冊です。 Newton(ニュートン) 19年 09 月号 雑誌 管理人おす
ニュートン 数学 微分積分のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス | 微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス | 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
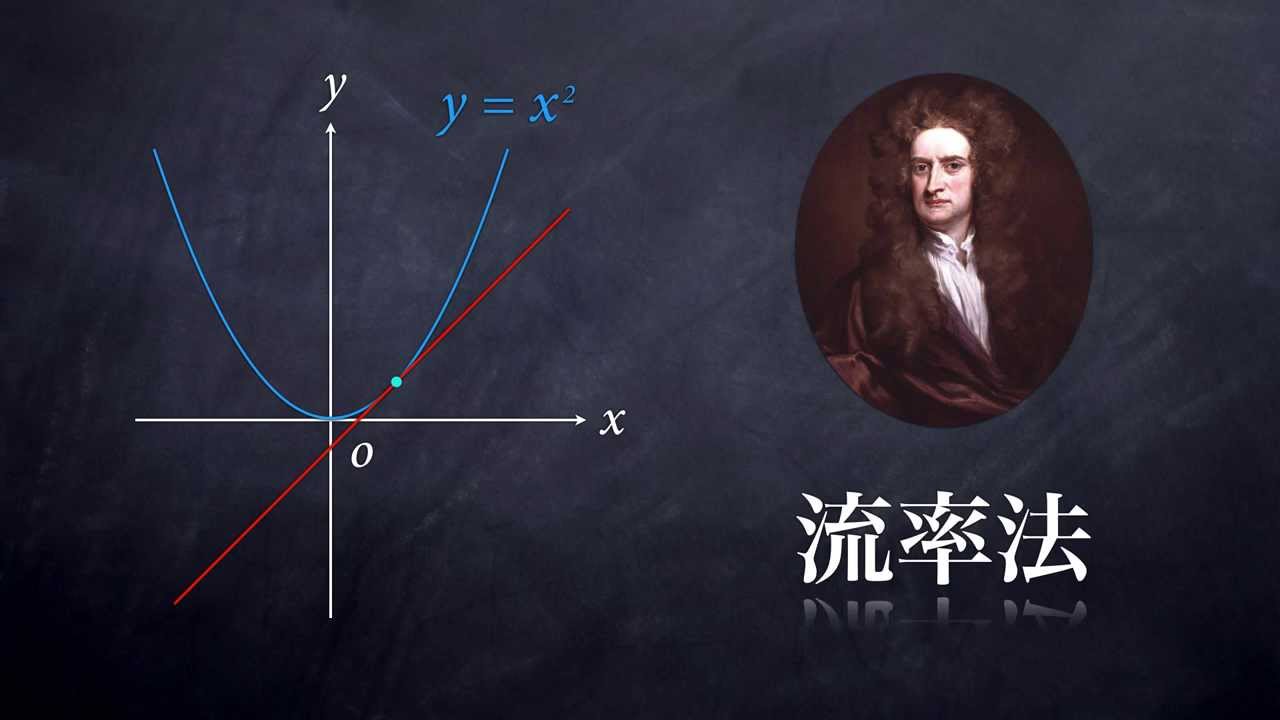 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス | 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス | 微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス | 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス | 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス | 微分と積分 改訂第２版 ニュートンプレス | 微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
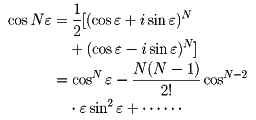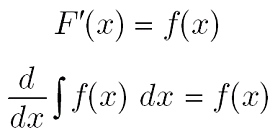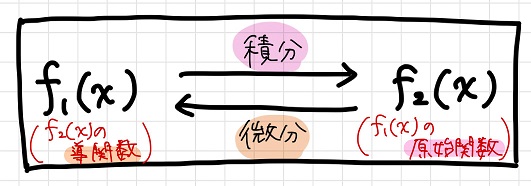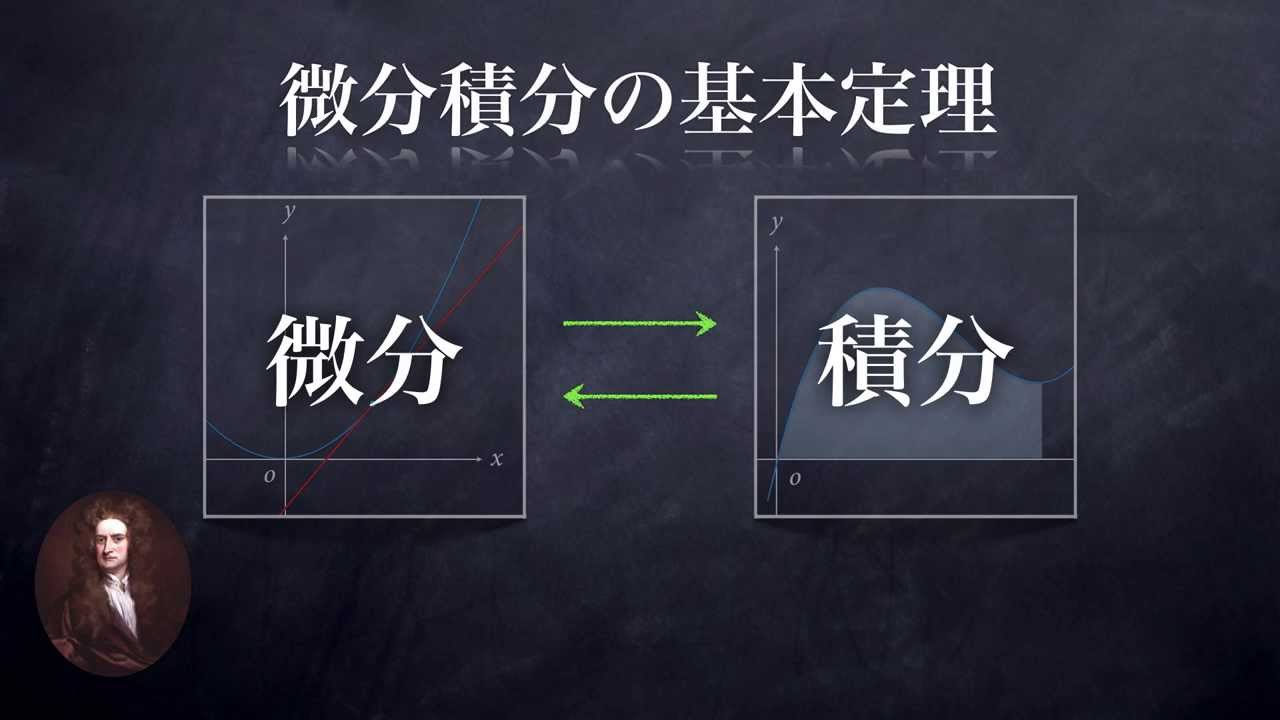 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |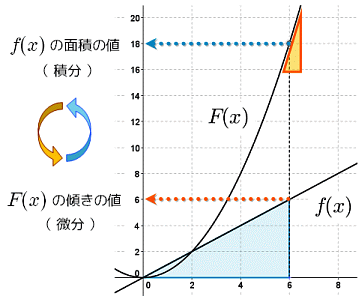
微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
「ニュートン 数学 微分積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
 微分と積分 改訂第２版 ニュートンプレス |  微分と積分 改訂第２版 ニュートンプレス |
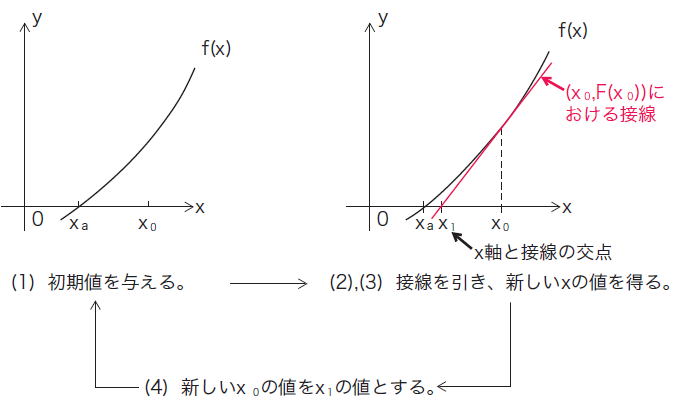
ラグランジュ記法とは、微分を微小量を表す記号を用いて分数のような形で表す方法である。 「ちょっと何言ってるか分からない」と思った人もいるだろう。 順番に説明していこう。 まず、微分の定義式 (1)式を見てもらいたい。 この式の分母は の微小 曲線または関数の傾きまたは導関数を計算するこのプロセスは、微分計算または微分と呼ばれます（または、ニュートンでは 用語、「流率の方法」–彼は、曲線上の特定のポイントでの瞬間的な変化率を「流率」と呼び、変化します。 の値 NS と y 「流暢」）。 たとえば、タイプの直線の導関数 NS ( NS) = 4 NS たった4です。 二次関数の導関数 NS ( NS) = NS2 は2です NS;
Incoming Term: ニュートン 微分積分, ニュートン 微分積分 発見, ニュートン 微分積分法, ニュートン 微分積分 ペスト, ニュートン 雑誌 微分積分, ニュートン 数学 微分積分,
0 件のコメント:
コメントを投稿